Fork me on GitHub

非极大值抑制NMS(Non-Maximum Suppression)

发表于 | 分类于 | | 次阅读
利用非极大值抑制算法(NMS)对生成的大量候选框进行后处理，去除冗余的候选框，得到最具代表性的结果，以加快目标检测的效率。

介绍

NMS顾名思义就是抑制不是极大值的元素，可以理解为局部最大搜索。这个局部代表的是一个邻域，邻域有两个参数可变，一是邻域的维数，二是邻域的大小。在目标检测中NMS主要用于提取分数最高的候选框。例如在用训练好的模型进行测试时，网络会预测出一系列的候选框，这时候可以用NMS来移除一些多余的候选框，即移除一些IOU值大于某个阈值的框。再比如在行人检测中，滑动窗口经提取特征，经分类器分类识别后，每个窗口都会得到一个分数。但是滑动窗口会导致很多窗口与其他窗口存在包含或者大部分交叉的情况。这时就需要用NMS来选取那些邻域里分数最高（是行人的概率最大）的窗口，并且抑制那些分数低的窗口。
NMS在计算机视觉领域有着非常重要的应用，如视频目标跟踪、数据挖掘、3D重建、目标识别以及纹理分析等等。

NMS在目标检测中的应用

去除重叠人脸检测框的例子


如上图所示，目的就是要去除冗余的检测框，找到最佳的候选框。

目标检测pipline中的例子


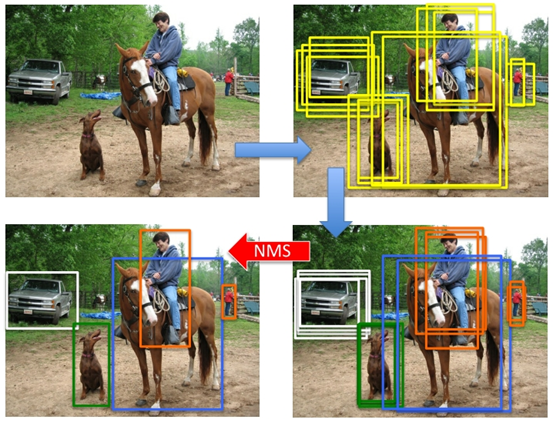
如上图所示，产生proposal后使用分类网络给出每个框的每类置信度，使用回归网络修正位置，最后使用NMS去除冗余的检测框。

NMS算法原理

对于bounding boxes列表B及其相应的置信度S，使用下述计算方式：选择具有最大score的检测框M，将其从B集合中移除并加入到最后的检测结果R中。通常将B中剩余检测框与M的IOU大于阈值threshold的框从B中移除。重复这个过程，直到B为空。
其中用到的排序，可以按照检测框右下角的坐标或者面积排序，也可以通过SVM等分类器得到的得分或概率进行排序，R-CNN中就是按照得分进行的排序。

比如上图，定位一个车辆的位置，算法找出了许多检测框，这时需要判断哪些矩形框是没用的。
非极大值抑制的方法是：先假设有6个矩形框，按照候选框的类别分类概率排序，假设属于车辆的概率排序结果为A < B < C < D < E < F。

  1. 先从最大概率矩形框F开始，分别判断A~E与F的IOU值是否大于某个设定的阈值；
  2. 假设B、D与F的重叠度超过设定的阈值，那么就移除B和D；并标记第一个矩形框F，是保留下来的。
  3. 从剩下的矩形框A、C、E中，选择概率最大的E，然后判断E与A、C的重叠度，如果重叠度大于设定的阈值，那么就扔掉；并标记E是保留下来的第二个矩形框。

就这样一直重复，直到找到所有被保留下来的矩形框。

Python源码实现

在R-CNN中使用了NMS来确定最终的bbox，其对每个候选框送入分类器，根据分类器的类别分类概率做排序(论文中称为greedy-NMS)。但其实也可以在分类之前运用简单版本的NMS来去除一些框。
python实现的单类别nms：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def py_cpu_nms(dets, thresh):
	""" Pure Python NMS baseline. """
	# x1、y1、x2、y2、以及score赋值
	x1 = dets[:, 0]
	y1 = dets[:, 1]
	x2 = dets[:, 2]
	y2 = dets[:, 3]
	scores = dets[:, 4]

	# 每一个候选框的面积
	areas = (x2 - x1 + 1) * (y2 - y1 + 1)
	# 按照score置信度降序排序
	order = scores.argsort()[::-1]

	keep = [] # 保留的结果框集合
	while order.size > 0:
		i = order[0]
		keep.append(i) # 保留该类剩余box中得分最高的一个
		# 计算当前概率最大矩形框与其他矩形框的相交框的坐标
		xx1 = np.maximum(x1[i], x1[order[1:]])
		yy1 = np.maximum(y1[i], y1[order[1:]])
		xx2 = np.minimum(x2[i], x2[order[1:]])
		yy2 = np.minimum(y2[i], y2[order[1:]])

		# 计算相交的面积，不重叠时面积为0
		w = np.maximum(0.0, xx2 - xx1 + 1)
		h = np.maximum(0.0, yy2 - yy1 + 1)
		inter = w * h
		#计算IoU：重叠面积 /（面积1+面积2-重叠面积）
		over = inter / (areas[i] + areas[order[1:]] - inter)

		# 保留IoU小于阈值的矩形框索引
		inds = np.where(over <= thresh)[0]
		# 将order序列更新，由于前面得到的矩形框索引要比矩形框在原order序列中的索引小1，所以要把这个1加回来
		order = order[inds + 1]

	return keep # 获取保留下来的索引

Faster R-CNN的MATLAB实现与python版实现一致，代码在这里:nms.m。另外，nms_multiclass.m是多类别nms，加了一层for循环对每类进行nms。

NMS loss

对多类别检测任务，如果对每类分别进行NMS，那么当检测结果中包含两个被分到不同类别的目标且其IoU较大时，会得到不可接受的结果。如下图所示：

一种改进方式是在损失函数中加入一部分NMS损失。NMS损失可以定义为与分类损失相同：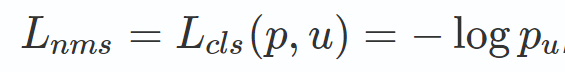

即真实类别u对应的log损失，p是C个类别的预测概率，相当于增加分类误差。
参考论文《Rotated Region Based CNN for Ship Detection》（IEEE2017会议论文）的Multi-task for NMS部分。

Soft-NMS

上述NMS算法的一个主要问题是当两个ground truth的目标的确重叠度很高时，NMS会将具有较低置信度的框去掉(置信度改成0)，如下图所示：

论文:《Improving Object Detection With One Line of Code》，改进之处：

改进方法在于将置信度改为IoU的函数：f(IoU)，具有较低的值而不至于从排序列表中删去。
（1）线性函数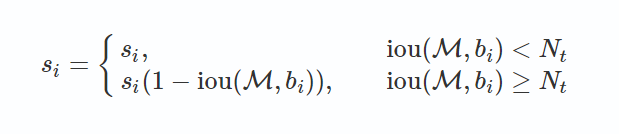

函数值不连续，在某一点的值发生跳跃。
（2）高斯函数

时间复杂度同传统的greedy-NMS，为O(N^2)。

Soft-NMS pythonPython源码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ua = float((x2 - x1 + 1) * (y2 - y1 + 1) + area - w * h)
ov = w * h / ua # iou between max box and detection box
if method == 1: # linear
    if ov > Nt:
        weight = 1 - ov
    else:
        weight = 1
elif method == 2: # gaussian
    weight = np.exp(-(ov * ov) / sigma)
else: # original NMS
    if ov > Nt:
        weight = 0
    else:
        weight = 1
# re-scoring 修改置信度
boxes[pos, 4] = weight * boxes[pos, 4]

在基于proposal方法的模型结果上应用比较好，检测效果提升：

在R-FCN以及Faster-RCNN模型中的测试阶段运用Soft-NMS，在MS-COCO数据集上mAP@[0.5:0.95]能够获得大约1%的提升详见这里。 如果应用到训练阶段的proposal选取过程理论上也能获得提升。对易重叠的目标类型确实有提高(目标不一定真的有像素上的重叠，切斜的目标的矩形边框会有较大的重叠)。而在SSD，YOLO等非proposal方法中没有提升。

其它应用

  • 边缘检测：
    ** Canny算子中的非极大值抑制是沿着梯度方向进行的，即是否为梯度方向上的极值点；参考这里
  • 特征点检测：
    ** 在角点检测等场景下说的非极大值抑制，则是检测中心点处的值是否是某一个邻域内的最大值。
0%